Stochastic Dominance
How do you compare 2 portfolios? Of course, you can use the Expected Value metric to compare these 2 portfolios. But 'expected value' cannot be used confidently to compare 2 portfolios or random variables all the time.
Why is Stochastic Dominance an important thing?
Stochastic Dominance is important for a risk-averse person. Imagine the following investment outcome.
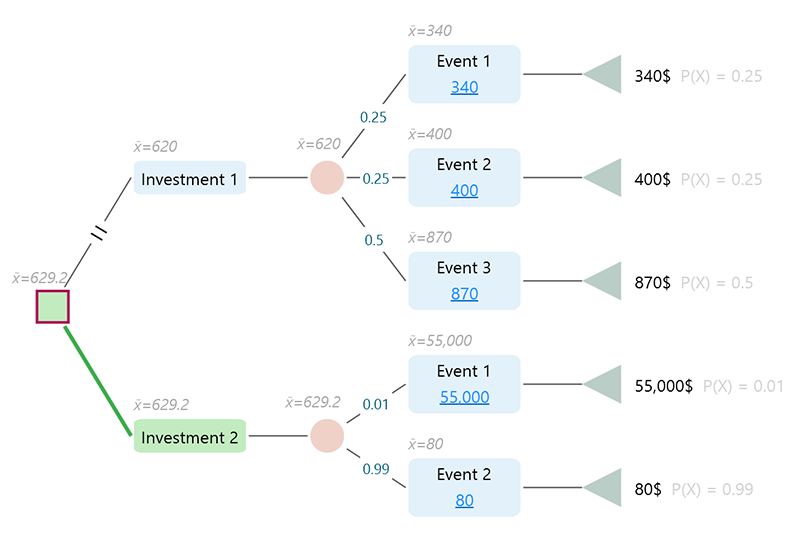
Notice that, Investment 1 has an expected value of 620$, and Investment 2 has an expected value of 629.2$. So, if you just consider a better-expected value means better decision, you may choose investment 2. So far so good. But, closely notice the outcomes with probabilities. Investment 2 gives 55,000$ with a 1% chance and 80$ with a 99% chance. On the contrary, Investment 1 has a better consistent outcome. You can earn at least 340$ for its lowest chance event, (25%). And for each event, you can expect a consistently better outcome. Unless you like gambling, you may not feel comfortable choosing investment 2 over investment 1 even though investment 2 gives better-expected value. Right? Investment 1 got something that just feels like a better option than investment 2. So, is there any mathematical way to find out if an option with a random outcome is better than another option with a random outcome where the process will consider a consistency type of thing? I mean, not just looking at the final expected value, is there any metric or calculation that will consider each outcome with probability and give you confidence about which option you should feel comfortable with? Yes, the answer is, "Stochastic Dominance".
Stochastic dominance will not tell an option with a lower expected value is better than an option with a higher expected value. That's the catch. If an option gets a higher expected value, you have to see the risk profile manually to make the decision. But, say, an option has a higher expected value than another option, then stochastic dominance will tell you if this higher expected value option is really and actually better than the lower expected value option considering individual outcomes with probabilities.
If you see an option that has a higher expected value than another option, but that winner option does not dominate the other option stochastically, then, think twice. That kind of winner option indicates a gamble-like situation. It is a good strategy to always check the stochastic dominance before making a final decision. Please note that stochastic dominance is important for a risk-averse person.
Notations
In the Decision Tree software and Rational Will, Stochastic dominance is calculated and displayed in the Stochastic Dominance Panel. You will see various notations as explained below:
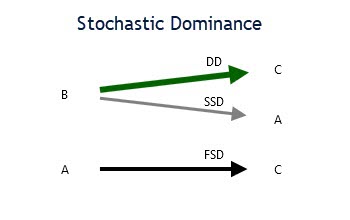
- FSD = First Order Stochastic Dominance.
- SSD = Second-Order Stochastic Dominance
- TSD = Third Order Stochastic Dominance
- DD = Deterministic Dominance
- μ σ = Mean-Variance Dominates
Here is an example view of the Stochastic Dominance Panel where A, B, C are various Actions.
First-Order Stochastic Dominance (FSD)
According to Wikipedia, Random variable A has first-order stochastic dominance over random variable B if, for any outcome x, A gives at least as high a probability of receiving at least x as does B, and for some x, A gives a higher probability of receiving at least x. In notation form, for all x
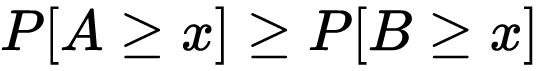
with strict inequality at some x.
We will explain this definition with an example. Consider the following scenario.
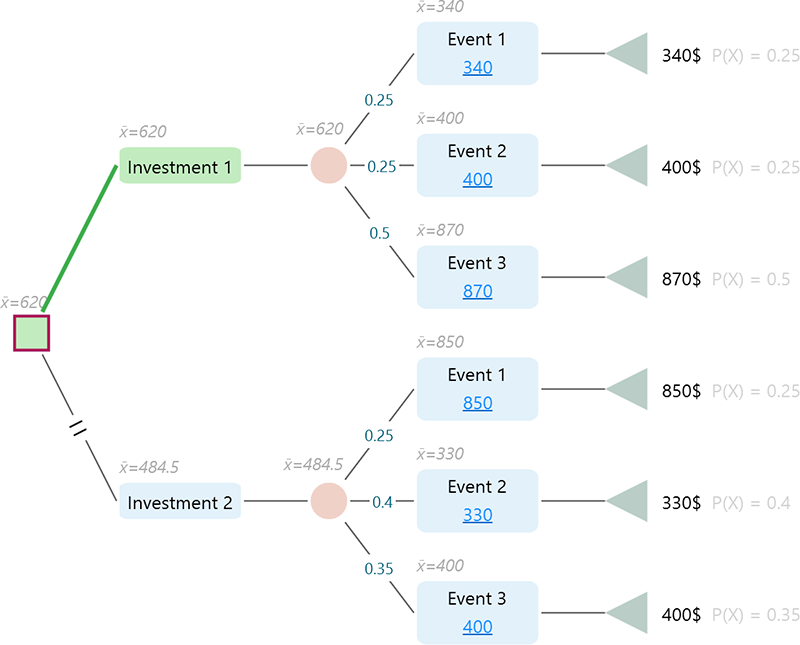
If you notice the Risk profile chart for this decision tree, you will see:
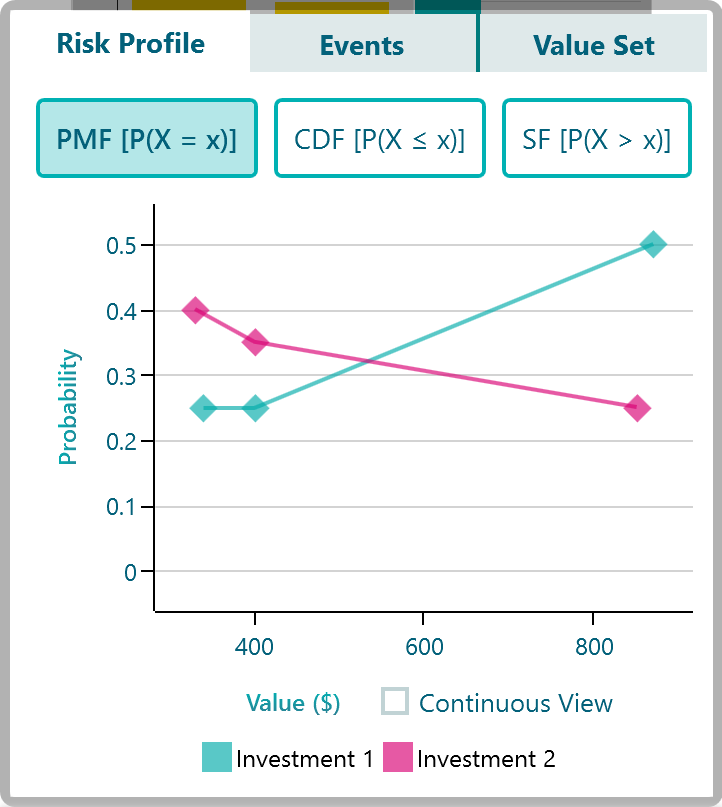
There is a button on the risk profile chart SF P (X > x). Click this button to see the survival probability distribution.
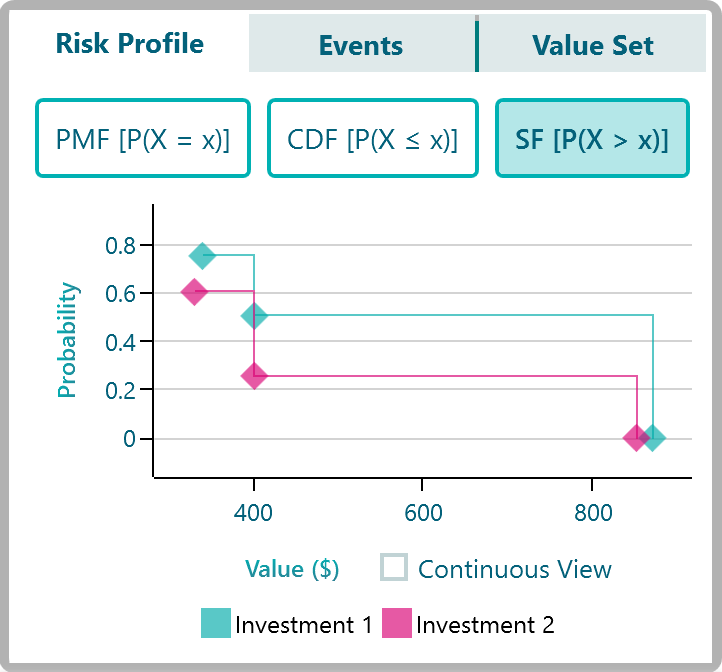
In the Survival function chart, observe around the payoff range 330$ - 340$. Check the probability of at least getting that payoff. Notice that, "investment 1" has a higher probability of 0.75 than investment 2 probability of 0.6. So, if you consider just that payoff range, you get a better chance of getting that payoff in Investment 1 than investment 2. Now check the payoff range around 400$. Yes, both of these investment has a payoff of 400$ with different probabilities. Notice that, the probability of getting at least 400$ with investment 1 is still higher, which is 0.5. For investment 2, the probability of getting at least 400$ is 0.25. So, for this payoff range, investment 1 ranks better again. Now, look at the payoff range of 850$-870$. Notice that, at least getting that payoff for both of these investments is 0%. Now, let's think about what we observed. Consistently "Investment 1" performed better than Investment 2 for each payoff segment. So, if both of these investment options are available, we can say, an investor may feel more comfortable choosing investment 1, not only because "investment 1" has better-expected value, but also "investment 1" gives a better payoff for a given probability.
So, we can see that "Investment 1" outranks "Investment 2" according to the first-order stochastic dominance.
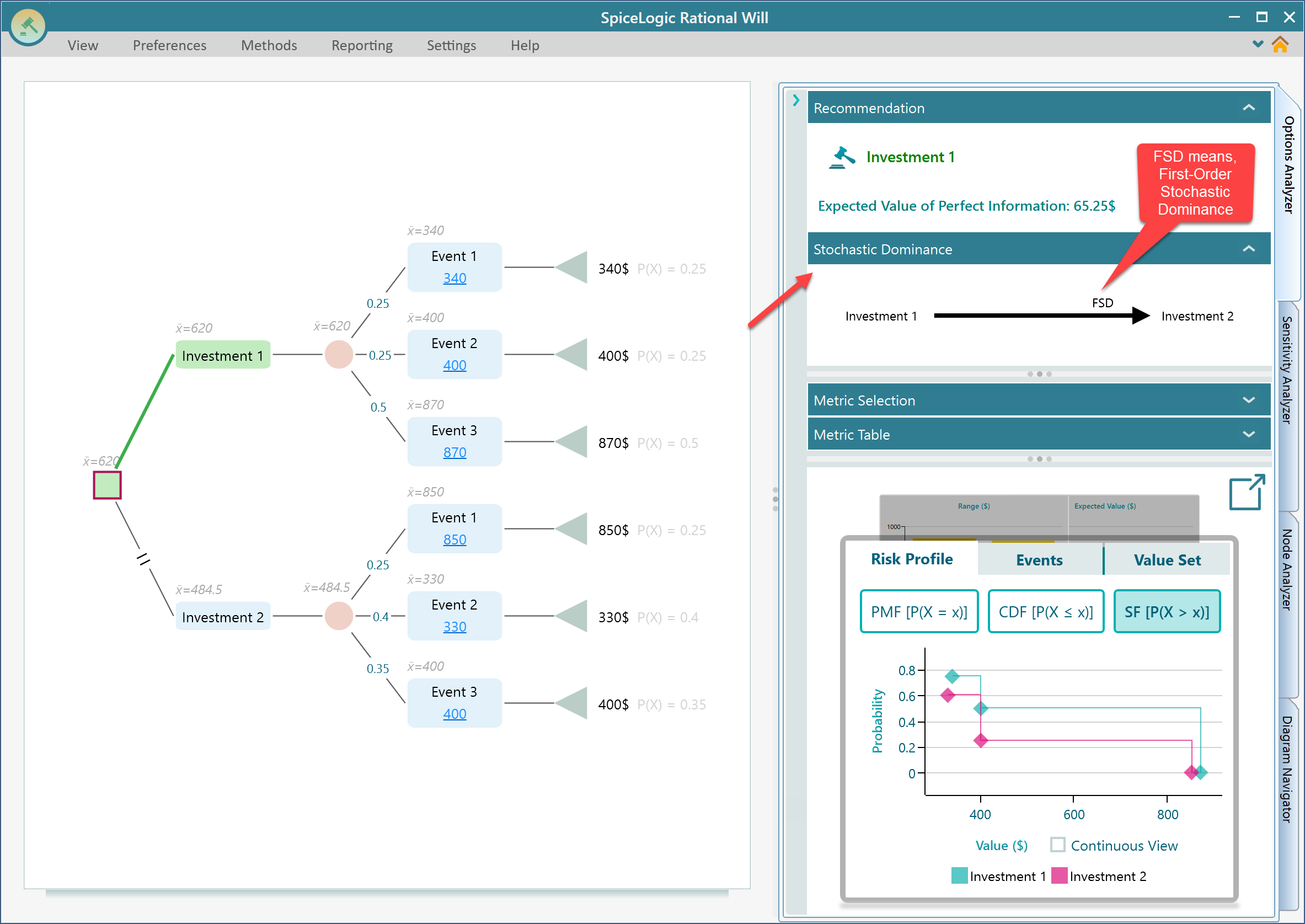
In the SpiceLogic Decision Tree software and Rational Will, you will see a dedicated panel for Stochastic dominance in the Options Analyzer section. Expand that panel and stochastical dominance will be calculated and displayed as a diagram. Notice the abbreviation "FSD" in the stochastic dominance panel. This FSD means, "First-Order Stochastic Dominance".
Second-Order Stochastic Dominance (SSD)
According to Wikipedia, For two gambles A and B, gamble A has second-order stochastic dominance over gamble B, if the former is more predictable (i.e. involves less risk) and has at least as high a mean. In notation form,
Let 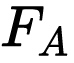 and
and 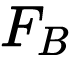 be the cumulative distribution functions of two distinct investments A and B. Then, For all payoff x:
be the cumulative distribution functions of two distinct investments A and B. Then, For all payoff x:
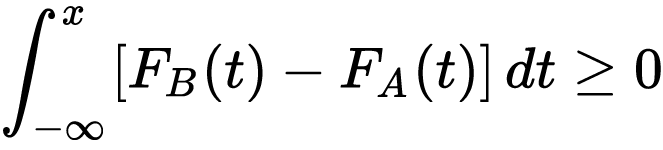
with strict inequality at some x.
So, what does all mean in simple layman's terms? I will try my way of explaining this in layman's terms. Notice that, in the case of First Order Stochastic dominance, when we observed that, for each payoff segment, the probability of getting at least that payoff segment is higher for the winner option. That makes the selection easy. But what if the other option which is not the winner, gives a better payoff at some segment and makes the choice more difficult? Mathematically, you may still choose that winner option until a point even when the other option gives a higher payoff at some probability. Aaah, I hear you. It sounds confusing. Right? Ok, let's cut straight. Just notice that the same old decision tree, I increased the payoff for Investment 2, Event 1, from 850$ to 1000$. Notice the expected value for Investment 2 increased and that makes investment 1 a little less attractive than before. But still, investment 1 is a better option stochastically. So, this time we say, "Investment 1" stochastically dominates "Investment 2" by second-order.
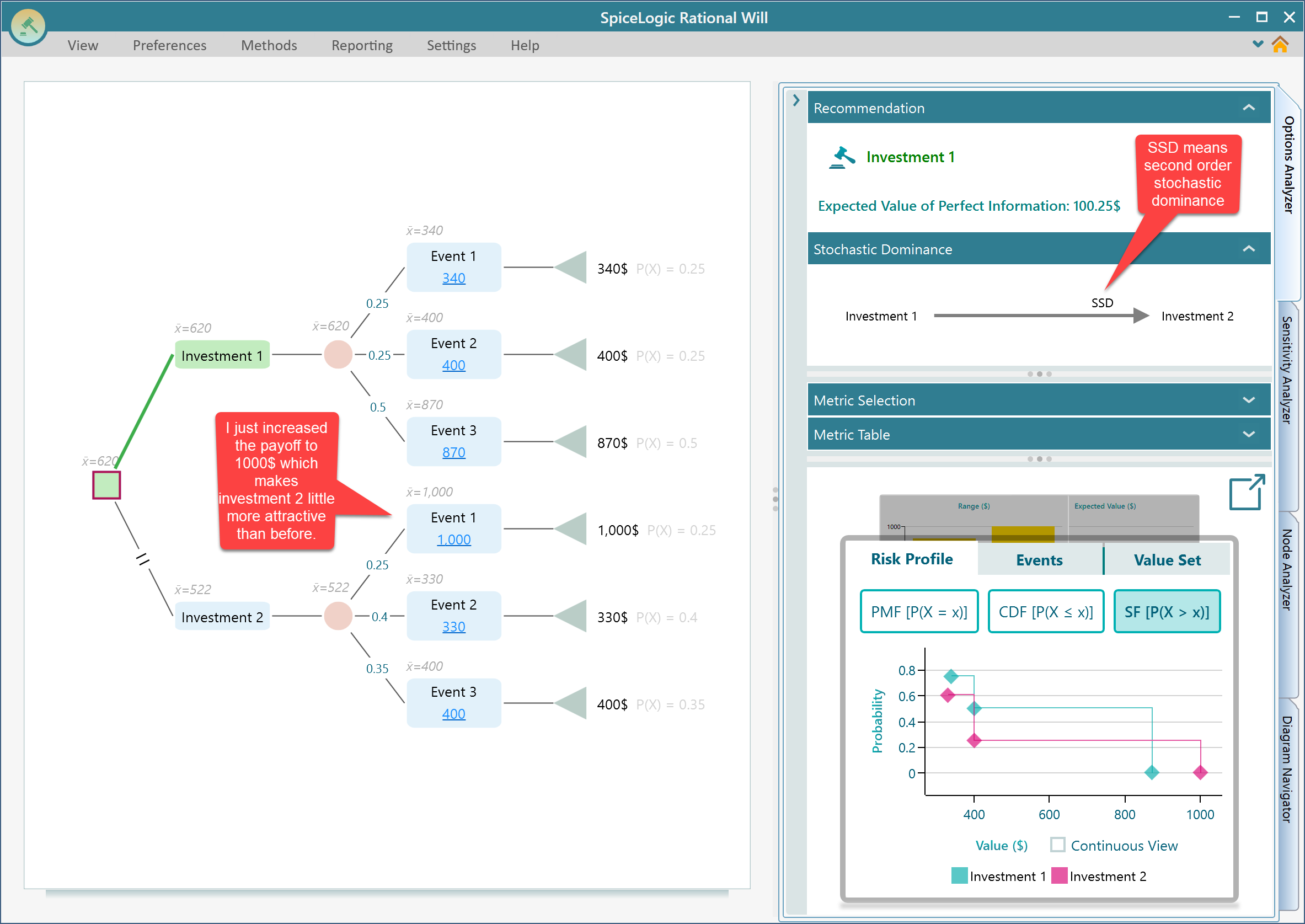
So, we learned that First-Order Stochastic dominance is better than Second-order stochastic dominance. But, if you do not find an option that dominates another one by the first order, but say, you found it dominates by second-order, you may consider that dominating option. it is a good thing that at least it stochastically dominates by second order.
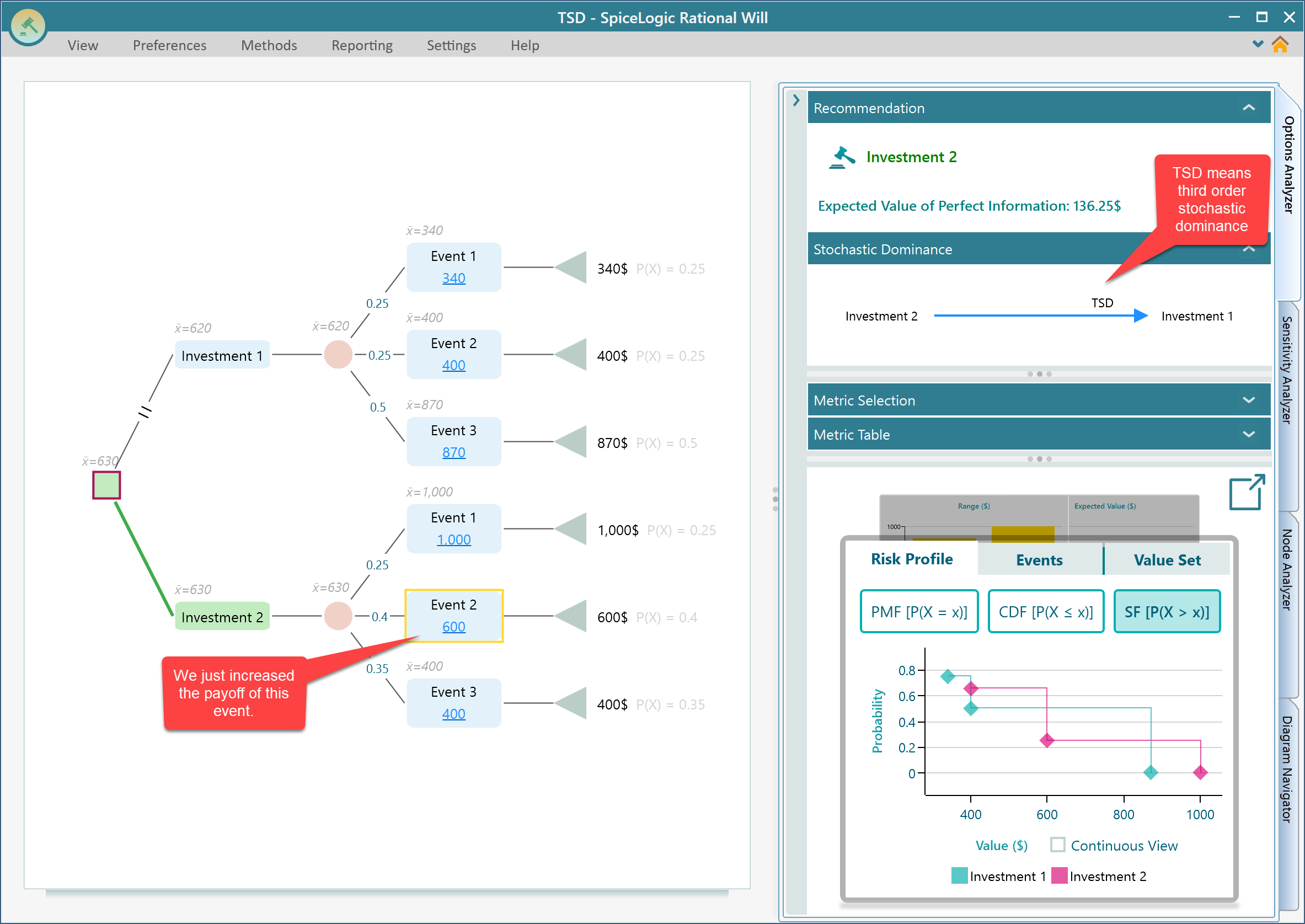
Third-Order Stochastic Dominance (TSD)
What we learned from second-order stochastic dominance is that it is just a weaker dominance compared to first-order dominance, right? We validated the idea by increasing a payoff of an event of the dominant option and then found that the FSD situation changed to SSD. The idea of Third-order stochastic dominance is that it is weaker than second-order stochastic dominance. That means, if you increase another payoff of the dominant option from the example of SSD, you will see the situation changes to Third-order stochastic dominance, as long as you do not change the payoff of a dominated option too high. We will demonstrate that idea with an example same as we did with SSD. But before that, let's see what Wikipedia says about Third Order Stochastic Dominance.
Let 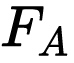 and
and 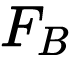 be the cumulative distribution functions of two distinct investments A and B. A dominates B in the third-order if and only if
be the cumulative distribution functions of two distinct investments A and B. A dominates B in the third-order if and only if
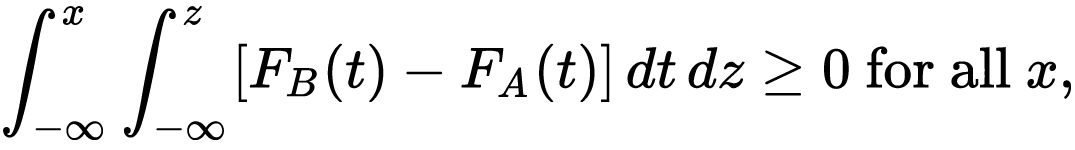
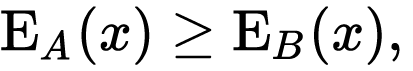
- And there is at least one strict inequality.
Let's give an example. Let's increase another event payoff as shown below. Now, investment 2 ranks higher than Investment 1 according to Expected value, but as Investment 1 was much a better option than Investment 2 before, by increasing that little payoff, Investment 2 looks better. But, not that better like FSD or SSD. This time, investment 2 outranks investment 1 by third-order stochastic dominance.
Other kinds of dominance
The Decision Tree software and Rational Will also shows some other kind of dominance, like
- Deterministic Dominance
- Mean-Variance Dominances
Deterministic dominance
Deterministic dominance is a straightforward easy to understand dominance. When say option A's minimum payoff is higher than option B's maximum payoff, then there is no question, you can say that Option A strongly dominates option B. And that type of dominance is called deterministic dominance. Here is an example.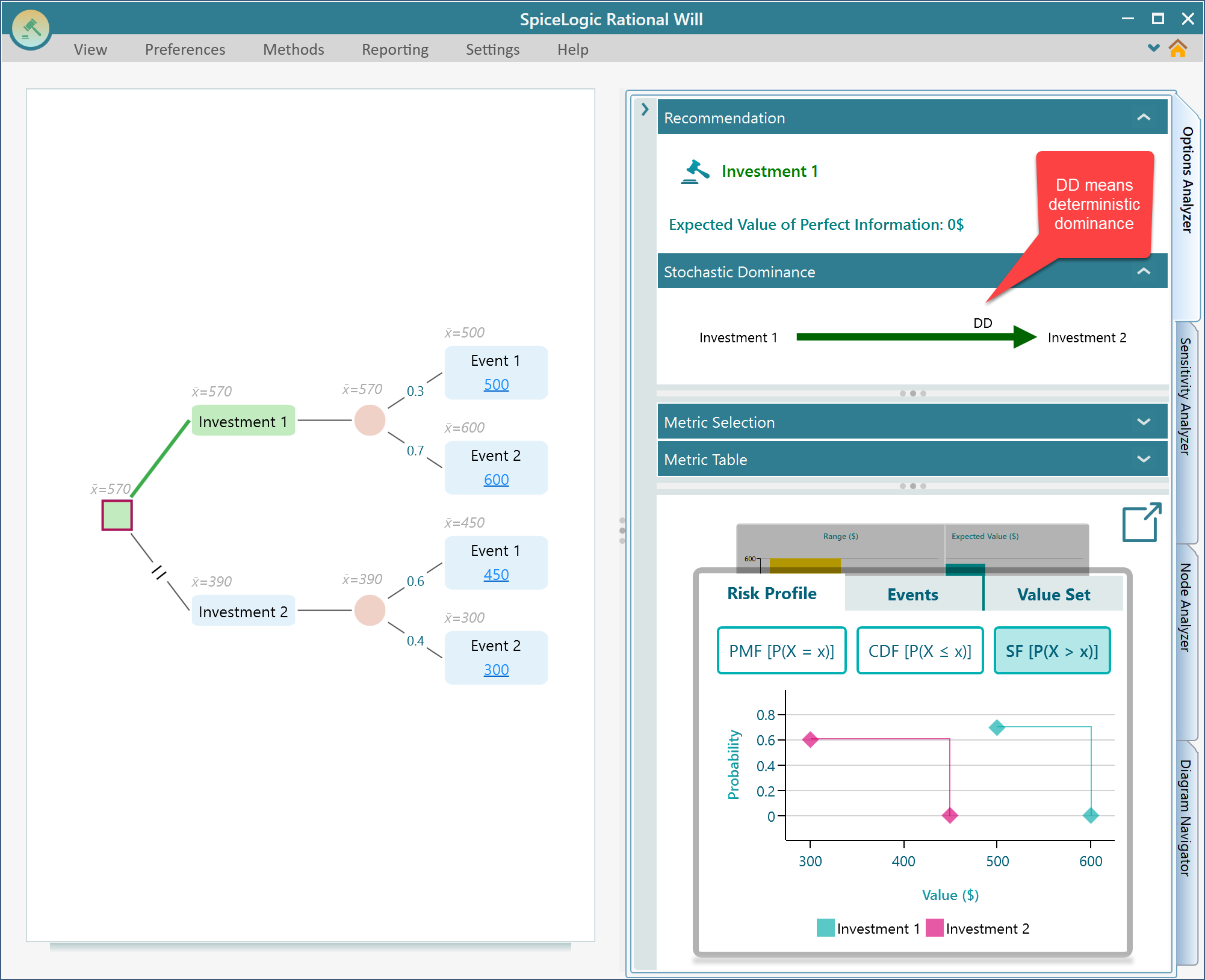
Mean-Variance Dominance
Many times, a stochastic dominance cannot be found between two random outcomes. In such cases, the SpiceLogic Decision Tree software and Rational Will software check if there is another way to determine one set of uncertainties are better than another set of uncertainties. And that is the "Mean-Variance" dominance. We know that a lotto or any other million-dollar lotteries are examples of a very high standard deviation. And only those who like to gamble will choose an option with a random outcome that has a very high standard deviation. Right? When comparing two options, an option with a lower standard deviation gives a more consistent outcome than the one that has a higher standard deviation. Say, an option named A has a higher expected value than option B. Also at the same time, option A has a lower standard deviation than option B. Obviously, in that case, Option A is better than Option B, not only because Option A has a better-expected value, but also it has lower variance. This kind of dominance is shown as "mean-variance" dominance in this software as shown below.
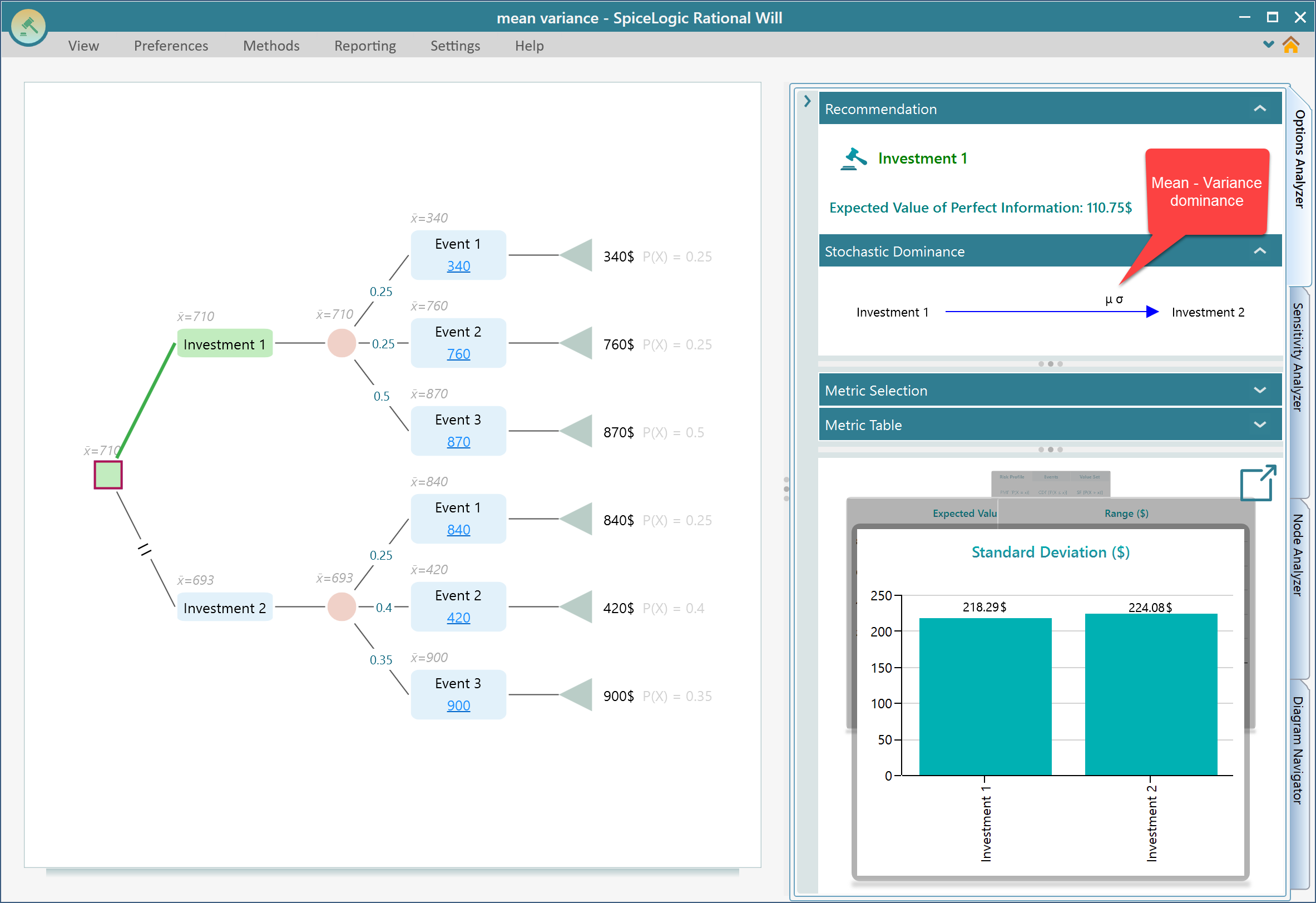
Note in the above screenshot, Investment 1 has an Expected value of 710$ and a standard deviation of 218.29$. Investment 2 has an expected value 693$ and a standard deviation 224.08$. So, Investment 1 dominates Investment 2 by mean-variance.
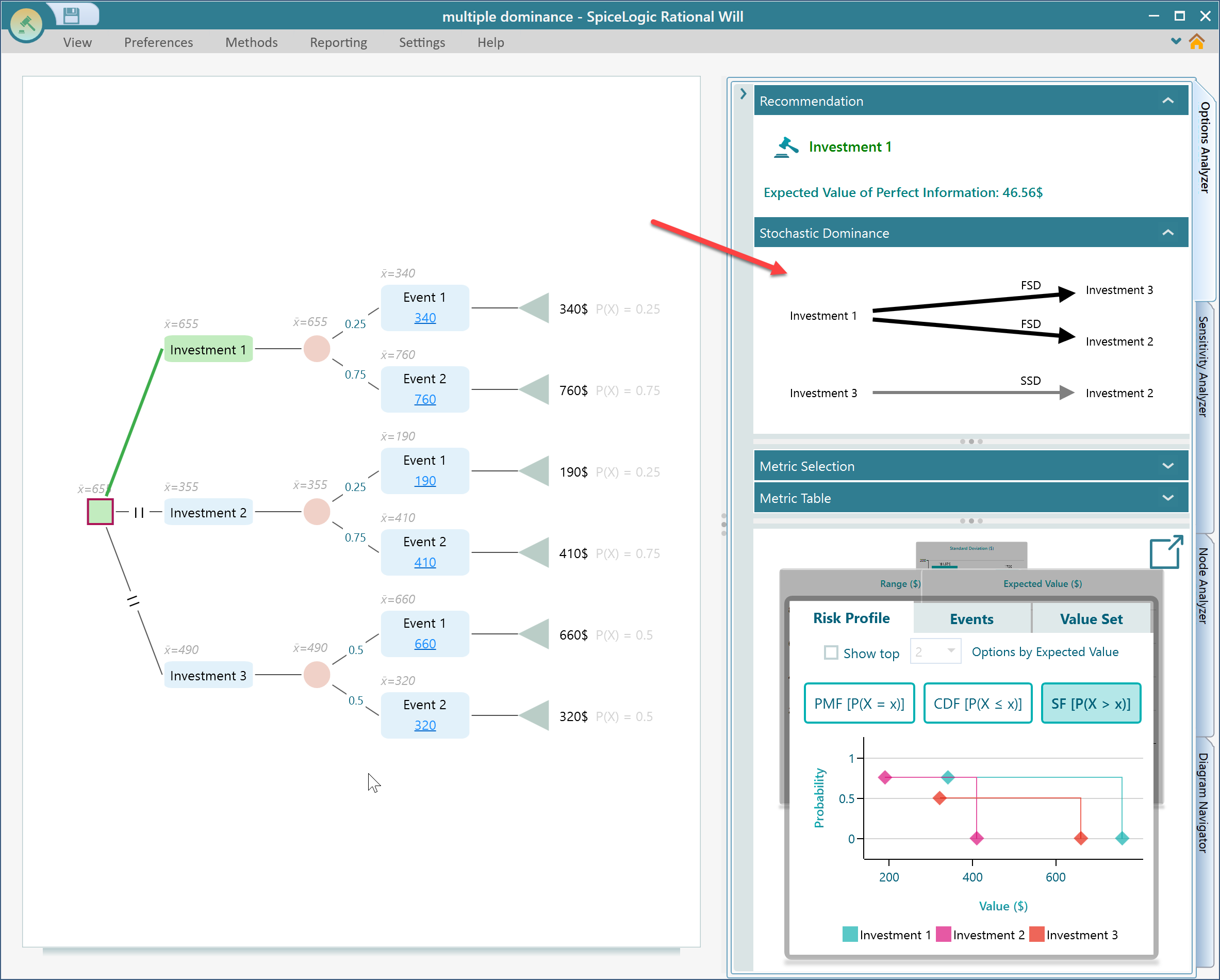
Multiple dominance in the same decision tree
If you have more than two options, then you may find one option dominates another option by first-order stochastic dominance and another option by second-order stochastic dominance. It becomes interesting to see how those options are dominating each other by what degrees. The SpiceLogic Decision Tree software and Rational Will software will show you a diagram of dominance like this.